Rob Welch

During 2021 I was lucky enough to spend a few months working as a senior research software engineer on MOLPRO, a quantum chemistry package that dates back to the 1960s. The post was only four months long due to disappearing EU funding, but it sounded like a fun thing to do between the end of my PhD and a more permanent research job, so I applied. MOLPRO calculates electronic structures – the wave functions and energies of quantum many-body systems. If you’ve ever seen one of those diagrams of electron shells that represent the wave functions as colourful balloons, then you’ll probably have some idea of what MOLPRO does. Physics is a series of abstractions that link together scales of distance and time. MOLPRO sits near the bottom of that ladder, but the parameterisations it creates can propagate up length scales in quite interesting ways. For example, energy in photosynthesis is generated by photoelectron transfer. MOLPRO can be combined with classical molecular dynamics simulations in order to study these systems.

Orbitals of triplet oxygen visualised in IQMol

Despite its relative antiquity, MOLPRO is still under very active development, and many parts of the codebase are extremely modern. MOLPRO implements a series of iterative solvers for linear and non-linear equations across distributed filesystems, contained in a package called LinearAlgebra. The first part means that the basic mathematical operations of the program (vector operations, matrix-vector operations, matrix-matrix operations) must be extremely fast. As the size of the problems in quantum chemistry get to be extremely large, often larger than available RAM, the other key optimisation is to ensure that the program is not bottlenecked by waiting for I/O, from memory or by waiting for the filesystem.

My approach to MOLPRO was two-pronged; first, work on tooling to better understand LinearAlgebra’s performance and profile to identify the code that the program spends the most time in. Second, to optimise the codebase in those key areas. MOLPRO is parallelisable with MPI, meaning it runs on multiple nodes of a supercomputer cluster. The nature of the numerics is such that most of the execution time is spent in deeply nested loops that call the same functions hundreds of thousands of times. For this reason, profiles generated by a general-purpose profiling tool such as Valgrind are not so useful, as they don’t account for the distributed computing environment and automatically-generated profiler calls can greatly distort the numerics. MOLPRO has a bespoke profiling library that’s designed to run with an incredibly low footprint and collect information from across MPI instances, but the output of the profiler was very limited (mostly text). One of the first things I did was to extend this profiler such that it could produce the familiar dotgraph format that can be interpreted by graphviz. These profiles were a lot easier to read, and this representation allowed me to merge profiler calls to the same function from different parts of the program, instead of displaying every part individually. This meant it was easier to find out the performance of the really low level operations that reoccurred all across the program. I am not a quantum chemist and a lot of the results didn’t make much sense to me, but I had the pleasure of working under Peter J. Knowles, who was able to interpret my profiles and tell me which parts of the program he thought were running too slowly.

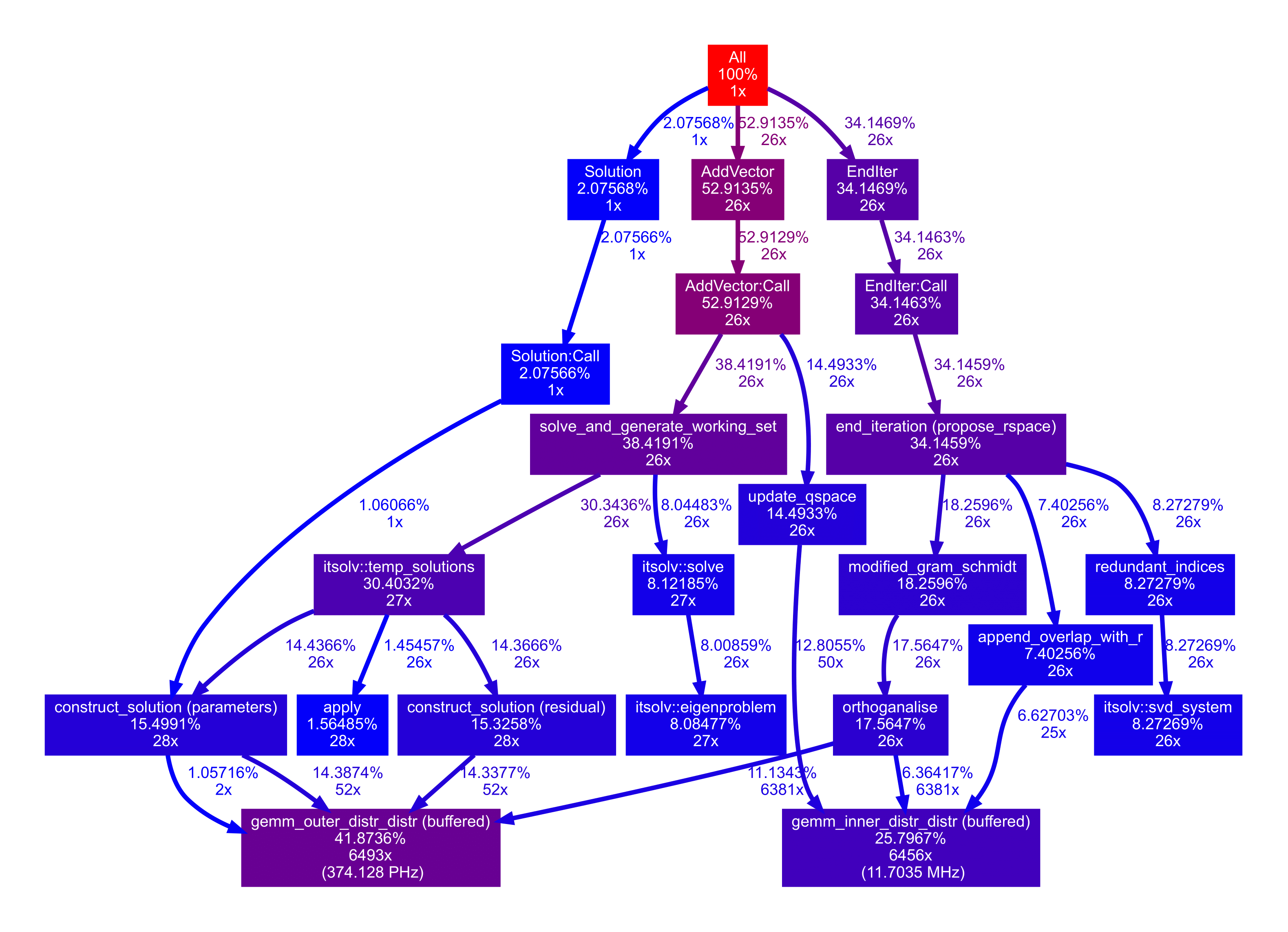
I was able to remove an unnecessary and very costly C++ implementation of the Gram-Schmidt algorithm in the eigenproblem solver, and also replaced calls to the Eigen library with calls to the (much faster) BLAS and Lapack libraries for other matrix\vector operations. These changes were very low-hanging fruit but accounted for a huge improvement in MOLPRO’s performance.

The other big change was to implement double-buffered disk I/O for the distributed data structures used in LinearAlgebra. Previously the program was blocked waiting for disk reads on very large files. When a matrix stored on disk was requested, the entire file would be loaded into memory before any operations were done (very slow and memory intensive). I implemented an I/O class that read these matrices from the disk in chunks, and asynchronously loaded the next chunk in the background. This meant that only the initial chunk-loading was completely blocked by I/O. I then reimplemented all of LinearAlgebra’s matrix and vector multiplication functions to use buffered chunks, and fed the chunked matrices into highly optimised BLAS/lapack library functions instead of using nested for loops and std::inner\outer product. I also added functionality to pick the optimal function based on the layout of the memory, e.g. if the memory has a consistent stride, a higher-level BLAS function is used (multiplying together entire matrices at once instead of iterating through them and multiplying vectors by matrices), which is faster.

Finally, I wrote a set of unit tests for the new code (the code coverage of MOLPRO’s linear algebra library is already extremely good), plus another set of profiler tools that run the program with a test system and plot the results, showing how the performance has improved:

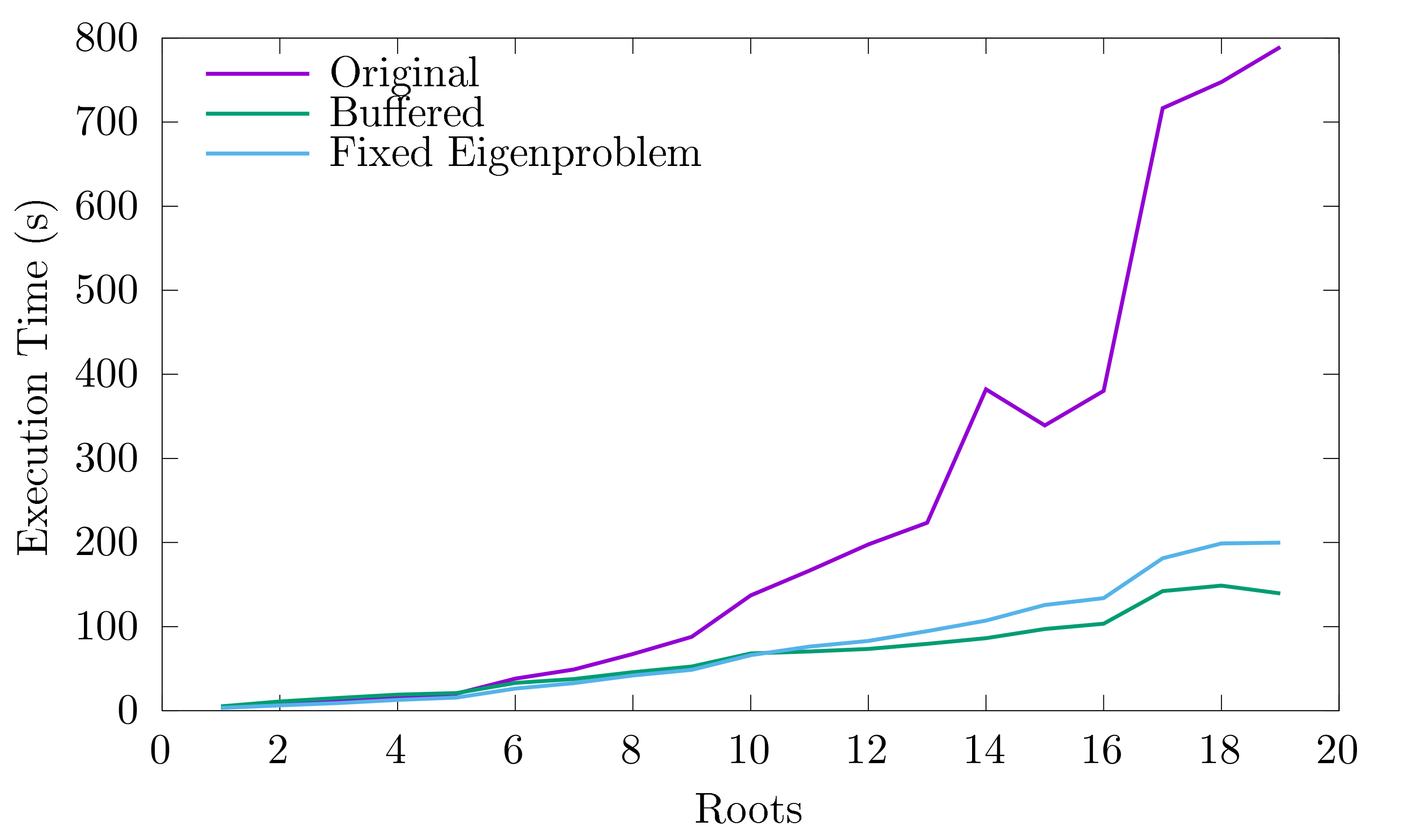
Scaling of LinearAlgebra’s performance with problem size (weak scaling). Original is the code as it was before I arrived, ‘Fixed Eigenproblem’ is the result of the numerical optimisations I made, ‘Buffered’ also includes the changes I made to the I/O. Before you get too excited, note that this is specifically the scaling of the LinearAlgebra library and not MOLPRO as a whole!

These changes are now in the MOLPRO development release and will likely land in MOLPRO 2022.1. Although MOLPRO is closed-source, the LinearAlgebra library is MIT-licensed, so you can check it out for yourself on gitlab: https://gitlab.com/molpro/linearalgebra

Last updated January 10, 2022.

Filed under: Physics, Software